A mérnöki világban egyre nagyobb hangsúlyt kapnak olyan témák, mint a mesterséges intelligencia vagy a mélytanuló algoritmusok. Óriási és kisebb számítástechnikai cégek is fektetnek ezekhez hasonló algoritmusokba, és életünket is egyre több helyzetben láthatatlan számítógépes szoftverek segítik. Jogosan merülhet fel a kérdés, hogy az algoritmusok által irányított világban hogyan alakulhat át a mérnöki tervezés.

Boronkay Gábor
Ez a folyamat nem most kezdődött a szakmában, és helyét a mai napig keresi, tendenciaként megfigyelhető azonban, hogy egyre több tervezőiroda egyre több ener-giát és pénzt fektet az építészet algoritmikus megközelítésébe. Az építészek is elkezdték a programozást úgy használni, mint egy tervezési eszközt; legyen szó koncepcióalkotásról vagy akár kiviteli tervek készítéséről. Sokszor nem is szükséges egy adott programozási nyelvet, mint például
a Pythont vagy a C#-ot megtanulni, mert az építészeti vizuális gondolkodáshoz közel álló vizuális programozási felületek is elérhetőek már. Erre jó példa a Grasshopper 3D alkalmazás is. Ezt a McNeel Rhinoceros CAD szoftverhez tartozó kiegészítőt használják olyan irodák is, mint a Zaha Hadid Architects, Norman Foster + Partners, Bjarke Ingels Group vagy a Thomas Heatherwick Studio. A vizuális programozás segítségével könnyen elérhetővé és használhatóvá válnak olyan misztikusnak tűnő algoritmusok, mint az evolúciós vagy mélytanuló programok. Sokszor hallhatjuk ezeket a kifejezéseket, de hogy valójában miről van szó és milyen módon hasznosíthatjuk lehetőségeiket, arról már ritkábban hallhatunk. Ebben az írásomban bemutatom, milyen lehetőséget nyújthatnak az evolúciós eljárások szerkezettervezés szempontjából, mikor érdemes használni azokat, és milyen szempontokat kell figyelembe venni alkalmazásuk közben.
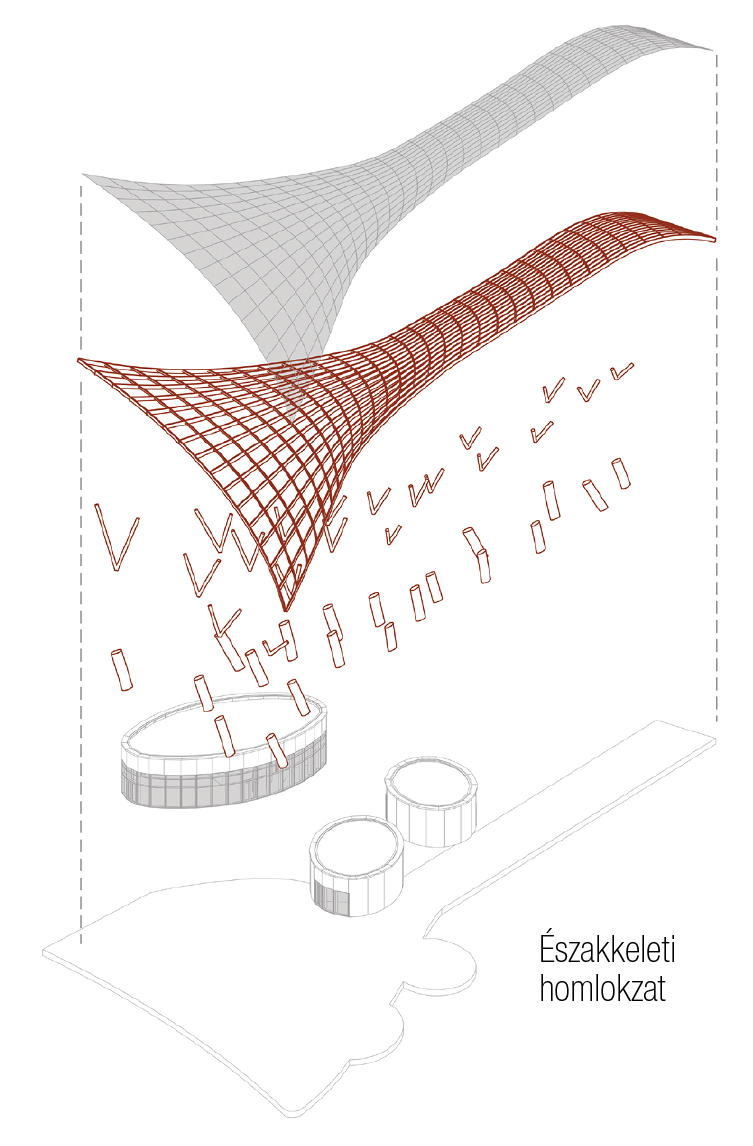
A téma körüljárásához a féléves -tervezési feladatomat használtam fel. A tervezés tárgya a fogaskerekű vasút új végállomása volt, ahol a kiszolgálóhelyiségek pavilonos elrendezésben kaptak helyet. Így merült fel az igény olyan tetőszerkezet iránt, ami egyszerre képes fedni a peront és a kiszolgálóépületek közötti gyülekezőként szolgáló teret. A megoldás végül egy kétszer görbült felület lett, ami egyszer vonal mentén, egyik sarkán pedig pontszerűen támaszkodik le. Az algoritmus ebből a felületből képezi a tető hierarchikus szerkezetét és a véletlenszerűnek tűnő oszlopos alátámasztást. A szelvényméreteket és az oszlopok pozícióját, dőlésszögét már evolúciós és végeselem módszerekkel definiáltam.
Fölmerülhet azonban a kérdés, hogy miért is hívják evolúciósnak ezt az eljárást?
Nevüket a természetben lejátszódó evolúciós folyamatokról kapták, mivel azok is hasonló szabályrendszerek szerint működnek. Ugyanúgy beszélhetünk az esetükben párzásról, öröklésről, mutációról és halálról. Először Lawrence J. Fogel írt ilyenfajta számítógépes eljárásokról az „On the organi–
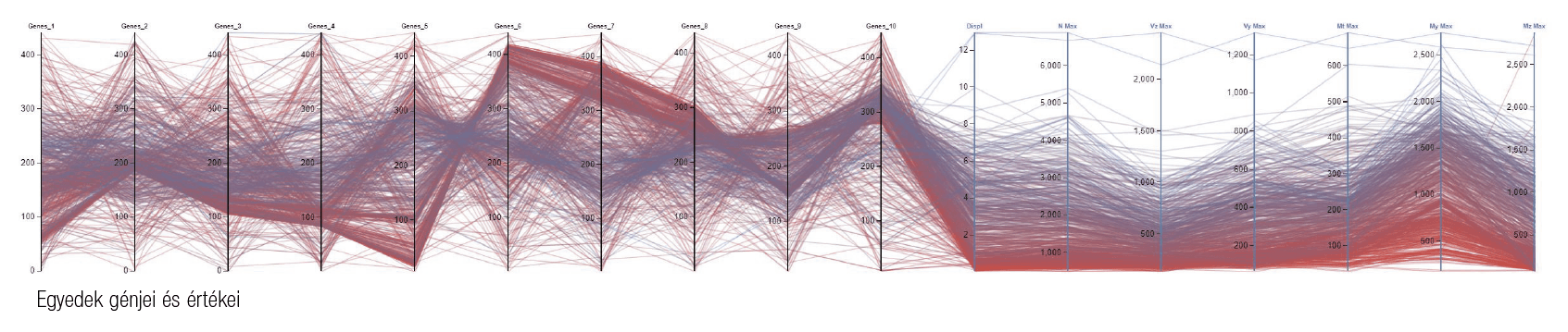
za-tion of the intellect” című publikációjá-ban 1964-ben. [1] Azóta ezen eljárások rendkívül sokat fejlődtek, és egyre inkább elterjedtek. Ahhoz viszont, hogy eredményesen alkalmazzuk őket, értenünk kell működésüket, továbbá pontosan meg kell fogalmaznunk, hogy mit szeretnénk megoldani. Egy adott probléma definiálásához szükségünk van egy mérőeszközre. Ebben segít a Fitness, azaz a megfelelőségi érték, amellyel osztályozni tudjuk az egyes egyedeket abból a szempontból, hogy mennyire teljesítenek az elvárásainknak megfelelően. Ez lehet számérték és függvény. Az egyszerűbb evolúciós eljárások az ilyen kritériumok értékből általában egyet tudnak figyelembe venni, de megjelentek már olyan eljárások is, amelyek egyszerre több ilyen megfelelőségi értéket is tudnak követni. [5] Azért beszélhetünk egyedekről, mert feladata elvégzéséhez az algoritmus véletlenszerű megoldásokkal áll elő, majd azokat értékeli a Fitness érték segítségével, és a legjobban teljesítő egyedeket (a különböző párosítási szabályoknak megfelelően) pároztatja, a legrosszabbul teljesítő egyedeket pedig megöli. Új, véletlenszerű egyedek létrehozása mellett ezt addig folytatja, amíg egy lokális vagy globális minimumot vagy maximumot el nem ér. Hasonlóan, mint a természetben lejátszódó evolúciós folyamatoknál. Ahhoz, hogy el tudjuk dönteni a végeredményről, hogy az a lehető legjobb végleges megoldást vagy csak kevésbé kielégítő, illetve részmegoldást jelent, szakértelem kell, felül kell azt vizsgálnunk. Az algoritmus alapvetően nem okos, csak rendkívül sok, akár több ezer lehetőséget végigpróbál helyettünk, és egy stratégia szerint igyekszik azt optimalizálni.
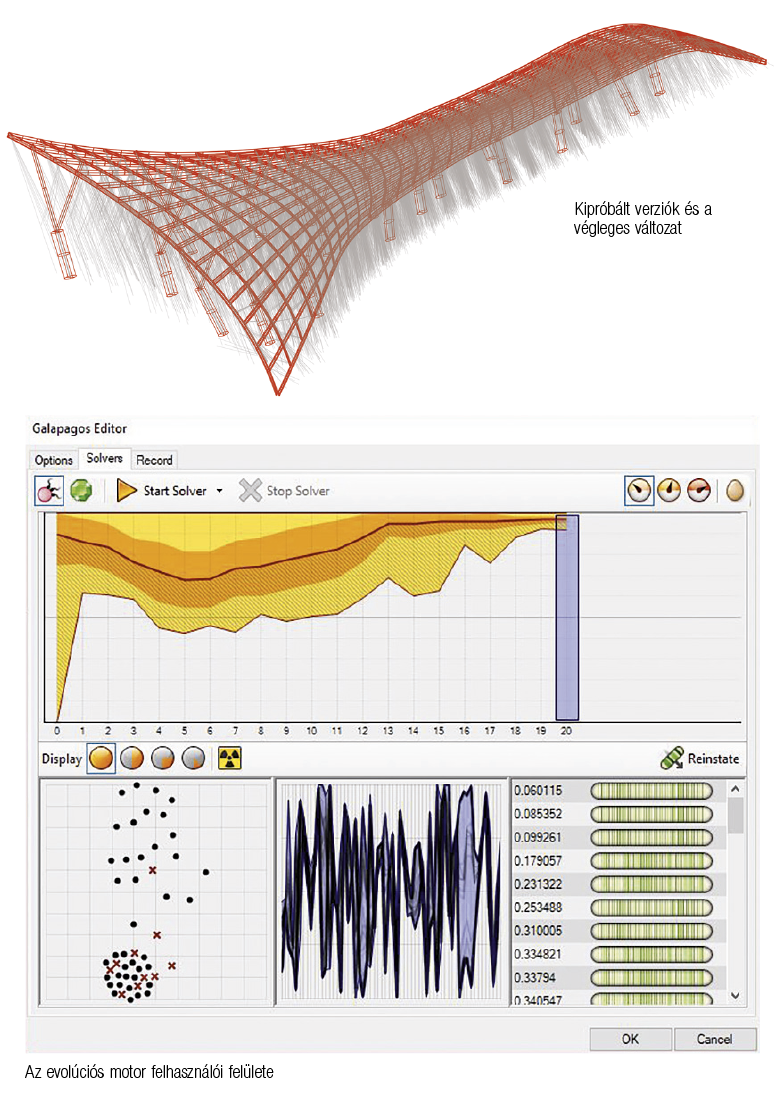
A saját tervemnél a szerkezet állékonyságának biztosításához használtam az eljárást. Ilyenfajta algoritmusok használatára a McNeel Rhinoceros 3D adott lehetőséget. Ezt egészítettem ki a Grasshopper 3D-vel, mely a parametrikus modellezést tette lehetővé, illetve magában tartalmazza a Galapagos evolúciós motort. Kiegészítettem még a szoftvert a Karamba 3D-vel, hogy létrejöhessen a végeselemes statikai szimuláció, illetve a Kangaroo-val, amely a formaoptimalizációt tette lehetővé. [4] Az algoritmus a szerkezet deformációja, azaz lehajlása alapján értékelt minden próbálkozást. Ezt az értéket a Karamba 3D-vel végzett analízis alapján kaptam, a tetőre ható szél-, hó- és önsúlyterhek alapján. Ez lett az algoritmus Fitness értéke, ez alapján törekedett a program a legjobb eredményre a 20 darab oszlop pozíciójának és dőlésszögének változtatásával. Ez viszont rendkívül sok változó paraméter, és így megnőtt a lehetősége annak is, hogy végeredményként csupán egy lokális minimumot kapunk a globális helyett. Ezt tudjuk ellensúlyozni a párosítási beállításokkal.
Ilyenfajta evolúciós eljárásoknál általában kétfajta pároztatásról beszélhetünk. A párosítás alatt azt az eljárást értjük, amikor a populációból kiválasztjuk, melyik kettő vagy több egyed genetikai állományát kombináljuk össze. Ezt tehetjük úgy, hogy egy adott egyedet a hozzá legközelebb elhelyezkedő leghasonlóbb egyedekkel párosítunk. Ilyenkor viszont azt kockáztatjuk, hogy a populációnk egy lokális optimumon fog ragadni. Egy másik megközelítés az úgynevezett zoophilic mating. Ilyenkor kizárjuk az adott egyedhez túl közel álló egyedeket, és ezzel növeljük a genetikai sokszínűséget. Ezt az eljárást több egyedre kivetítve jól lehatárolható fajokat kapunk, ahol mindegyik populáció a saját optimumát keresi, és ezzel nagyobb szórásban vizsgáljuk az adott problémát. Optimálisnak tűnő megoldás az lenne, hogy megpróbáljuk elkerülni a beltenyészetet, de kontrollálni tudjuk a túlzottan távoli párosodást is – elkerülve a túl véletlenszerű, zajos eredményeket. Emellett képesek vagyunk beállítani, hogy mekkora populáció mellett szeretnénk dolgozni, azaz egy adott generáció hány tagot tartalmazzon, ezzel is csökkentve az esélyét, hogy egy lokális minimumon maradjon az eljárás. Ha egy megoldáshoz közel járunk az algoritmus futtatása előtt, akkor beállíthatjuk, hogy hány százalékban örököljenek az új generációk a kezdőtől, illetve mekkora legyen az öröklés százaléka. [3] Saját példámban a legjobb eredményeket akkor értem el, amikor az algoritmust először zoophilic pároztatással futtattam nagy populációszám mellett, hogy megtalálja a globális maximum lehetséges szintjét, majd minél közelebbi egyedeket pároztattam, hogy a globális maximum környékén a lehető legjobb eredményeket garantálhassam.
Ezekről az evolúciós eljárásokról tudni kell, hogy rendkívül sok időt vehetnek igénybe, és a parametrikus szkript felépítésétől függően nagyon sok számítási kapacitásra is szükség lehet. Ám még így is rendkívül sok lehetőséget vagyunk képesek velük tesztelni. Előnyük az is, hogy nem szükséges a végeredményt elfogadnunk, mint legjobbat, hanem részeredményeket is kiragadhatunk, felülvizsgálhatunk és eredményként felmutathatjuk. Így valójában az összes kipróbált verziót átértékelhetjük. Az én kísérleteim során a legjobban teljesítő algoritmus két napig futott, és 112 generációt hozott létre, ami közel 6000 egyedi kipróbált állapotot jelent. Tervezésem során ezekkel az eljárásokkal tudtam biztosítani, hogy egy irreguláris, azaz szabálytalan, elemi függvényekkel nem, vagy nehezen leírható felülethez – az azt érő terheket és a szerkezetben ébredő erőjátékokat is figyelembe véve – egy megvalósítható, optimális szerkezetet hozhassak létre.
Ehhez szükséges volt az a parametrikus környezet, amelyben definiálni tudtam a teljes tetőgeometriát, így biztosítva azt, hogy minden verzión gyors méréseket tudjak végezni. Az ilyen parametrikus felületek előnye, hogy komolyabb programozási tudás nélkül, gyorsan vagyunk képesek geometriákat definiálni, és azokat különböző kiegészítők segítségével optimalizálni, mérni. A Grasshopperen belül képesek lehetünk olyan láncmodellek felállítására másodpercek alatt, mint amilyeneket Antoni Gaudí, Barcelona egyik legmeghatározóbb építésze is használt saját 19. századi szerkezeteinek optimalizálására. De közelebb is találunk példát hasonló törekvésekre: a nemrég Pritzker-díjat nyert Iszozaki Arata is előszeretettel használ úgynevezett XESO [1] eljárásokat, ezeket szintén könnyedén reprodukálhatjuk ebben a fejlesztői környezetben. Így ezek az eszközök rendkívül nagy segítséget jelenthetnek egy mind építészeti, mind más szakági szempontból megfelelő koncepció felállítására. Nem muszáj csak tartószerkezeti szempontokat figyelembe vennünk, ugyanúgy állíthatunk energetikai, gépészeti kritériu-mokat is a programnak, hiszen erőssége a rugalmasságában, moduláris felépítésé-ben rejlik. A kivitelezés folyamatát is megkönnyítheti egy jól felépített algoritmus, ehhez viszont már a tervezési fázis elején számításba kell venni képességeit, és megfelelő stratégiát kell felállítani. Más iparágakban is egyre nagyobb szerepet kapnak a hasonló fejlesztői környezetek és eljárások, egyre több és jobban teljesítő hasonló algoritmusról beszélhetünk. Elkezdtek megjelenni olyan példák is, ahol különböző megoldómotoroknak különböző munkafázist szánnak, így is optimalizálva a végeredményeiket. [2] Véleményem szerint az építészetnek is javára válhat, ha odafigyel ezekre az eljárásokra és megpróbálja a munkafolyamatokba integrálni. Az in-tuíciónkat nem helyettesíti a tervezés során, hiszen a megfelelő kérdéseket még mindig nekünk kell feltenni, csupán a döntésünket segítheti, olyan mederbe terel-heti a tervezés folyamatát, amilyet az elején nem is sejtettünk volna.
Forrás:
1. Tedeschi, Arturo. 2014. AAD_ Algorithms Aided Design. Olaszország: Le Penseur Publisher, 2014.
2. Domingos, Pedro. 2015. The Master Algorithm. 1. Anglia: Penguin Books, 2015.
3. Rutten, David. 2011. I Eat Bugs For Breakfest. [On-line] 2011. https://ieatbugsforbreakfast.wordpress.com/
4. Pugnale, Alberto. 2006-2018. albertopugnale. [On-line] 2006-2018. http://www.albertopugnale.com/
5. Computational Morphogenesis in architecture: structure and light as a multi-objective -design/optimization problem. Allesandro Liuti, Alberto Pugnale, Alessio Erioli. 2013.














